SVM

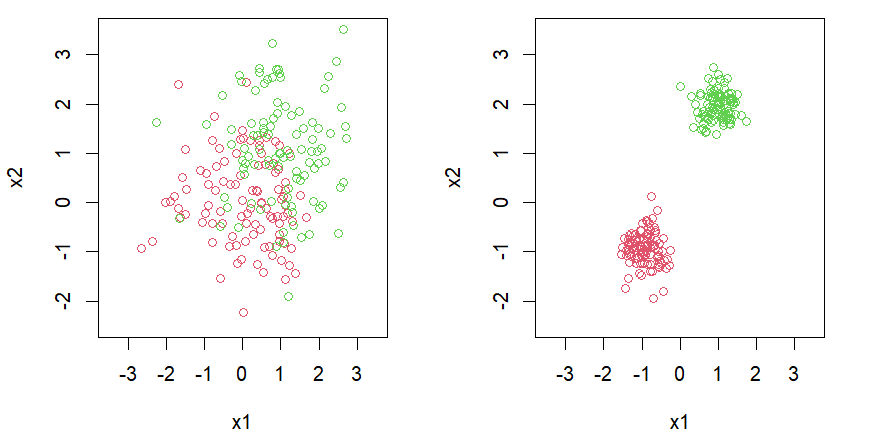
Linear Separable

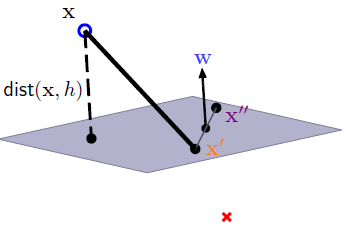
$$\begin{align*} \forall i,\ y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) > 0 \end{align*}$$

Distance

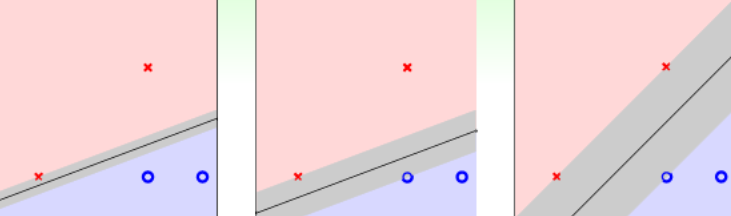
$$\begin{align*} \Rightarrow \ & \underset{\sim}{w}^T( \underset{\sim}{x}^{''} - \underset{\sim}{x}^{'} )=0 \\\\\\ \Rightarrow \ &\text{dist}( \underset{\sim}{x}, b, \underset{\sim}{w}) = \left| \frac{\underset{\sim}{w}^T}{ \left| \underset{\sim}{w} \right|} (\underset{\sim}{x} - \underset{\sim}{x^{'}}) \right| = \frac{1}{\left| \underset{\sim}{w} \right|} \left| \underset{\sim}{w}^T \underset{\sim}{x} + b \right| \end{align*}$$

SVM

Hyperplane $\underset{\sim}{w}^T \underset{\sim}{x} + b$ and data point $\underset{\sim}{x_i}$ with label $y_i$

$$\begin{align*} \underset{b,\underset{\sim}{w}}{\text{arg max}} & \left( \text{margin}(\underset{\sim}{w},b) \right) \text{ subject to } \forall i,\ y_i ( \underset{\sim}{w}^T \underset{\sim}{x_i} + b) > 0 \end{align*}$$$$\begin{align*} \text{margin}(\underset{\sim}{w},b) = \min_i \text{dist}(\underset{\sim}{x_i},\underset{\sim}{w},b) = \min_i \frac{1}{\left| \underset{\sim}{w} \right|} \left| \underset{\sim}{w}^T \underset{\sim}{x_i} + b \right| \end{align*}$$$$\begin{align*} \underset{b,\underset{\sim}{\textcolor{orange}{w}}}{\text{arg max}} & \left( \frac{1}{\left| \underset{\sim}{\textcolor{orange}{w}} \right|} \min_i y_i (\underset{\sim}{{\textcolor{orange}{w}}^T} \underset{\sim}{x_i} + \textcolor{orange}{b}) \right) \\\\\\ & \text{subject to } \forall i,\ y_i ( \underset{\sim}{{\textcolor{orange}{w}}^T} \underset{\sim}{x_i} + \textcolor{orange}{b}) > 0 \end{align*}$$

Let $\displaystyle \min_i y_i(\underset{\sim}{\textcolor{orange}{w}}^T \underset{\sim}{x_i} + \textcolor{orange}{b})=k$, then \quad $\displaystyle \min_i y_i({\underset{\sim}{\textcolor{orange}{w}}^T \frac{1}{k}} \underset{\sim}{x_i} + {\frac{\textcolor{orange}{b}}{k}} )=1$

Denote ${\underset{\sim}{\textcolor{orange}{w}}^T \frac{1}{k}}$ as $\textcolor{red}{\underset{\sim}{w}^T}$, $\frac{\textcolor{orange}{b}}{k}$ as $\textcolor{blue}{b}$

$$\begin{align*} \Leftrightarrow \ \underset{b,\underset{\sim}{w}}{\text{arg max}} \left( \frac{1}{\left| \underset{\sim}{w} \right|} \right) \quad \text{subject to } \min_i y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) = 1 \end{align*}$$$$\begin{align*} & \underset{b,\underset{\sim}{w}}{\text{arg max}} \left( \frac{1}{\left| \underset{\sim}{w} \right|} \right) \text{subject to } \min_i y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) = 1 \\\\\\ \end{align*}$$

If optimal $(\textcolor{orange}{b},\underset{\sim}{\textcolor{orange}{w}})$ with $\min_i y_i (\underset{\sim}{\textcolor{orange}{w}}^T \underset{\sim}{x_i} + \textcolor{orange}{b}) = k>1$, we can scale $(\textcolor{orange}{b},\underset{\sim}{\textcolor{orange}{w}})$ to $({\frac{\textcolor{orange}{b}}{k}} ,{\frac{\underset{\sim}{\textcolor{orange}{w}}}{k}} )$

$$\begin{align*} \Leftrightarrow \ & \underset{b,\underset{\sim}{w}}{\text{arg max}} \left( \frac{1}{\left| \underset{\sim}{w} \right|} \right) \text{subject to } \forall i, \; y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) \geq 1 \end{align*}$$$$\begin{align*} & \underset{b,\underset{\sim}{w}}{\text{arg max}} \left( \frac{1}{\left| \underset{\sim}{w} \right|} \right) \quad \text{subject to } \forall i, \; y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) \geq 1 \\\\\\ \Leftrightarrow \ &\underset{b,\underset{\sim}{w}}{\text{arg min}} \left( \frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} \right) \quad \text{subject to } \forall i, \; 1-y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) \leq 0 \end{align*}$$

Let $\displaystyle L=\frac{1}{2} \underset{\sim}{w}^{T} \underset{\sim}{w} + \sum_{i=1}^{N} \lambda_{i}\left(1-y_{i}\left(\underset{\sim}{w}^{T} \underset{\sim}{x_i} +b\right)\right)$, and we claim that

$$\begin{align*} & \underset{b,\underset{\sim}{w}}{\text{arg min}} \left( \frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} \right) \quad \text{subject to } \forall i, \; 1-y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) \leq 0 \\\\\\ \Leftrightarrow \ & \displaystyle \underset{b, \underset{\sim}{w}}{\text{arg min}} (\ \max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right)) \end{align*}$$$$\begin{align*} & \underset{b,\underset{\sim}{w}}{\text{arg min}} \left( \frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} \right) \quad \text{subject to } \forall i, \; 1-y_i (\underset{\sim}{w}^T \underset{\sim}{x_i} + b) \leq 0 \\\\\\ \Leftrightarrow \ & \displaystyle \underset{b, \underset{\sim}{w}}{\text{arg min}} (\ \max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right)) \end{align*}$$

Violating $(b, \underset{\sim}{w})$: \\\

\qquad \qquad $\displaystyle \max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right) = \max _{\forall \lambda_{i} \geq 0} \frac{1}{2} \underset{\sim}{w}^{T} \underset{\sim}{w} + \sum_{i=1}^{N} \lambda_{i} (\textcolor{blue}{\text{positive}})$

Feasible $(b, \underset{\sim}{w})$: \\\

$$\begin{align*} &\max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right) \geq L\left(b, \underset{\sim}{w}, \lambda_{i}^{*} \right), \quad \text{for some } \lambda_{i}^{*} \\\\\\ \Rightarrow \ & \min _{b, \underset{\sim}{w}}\left(\max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right)\right) \geq \min _{b, \underset{\sim}{w}} L\left(b, \underset{\sim}{w}, \lambda_{i}^{*} \right), \quad \text{for some }\lambda_{i}^{*} \\\\\\ \Rightarrow \ & \min _{b, \underset{\sim}{w} }\left(\max _{\forall \lambda_{i} \geq 0} L\left(b, w, \lambda_{i}\right)\right) \geq \max _{\forall \lambda_{i} \geq 0} \left(\min _{b, \underset{\sim}{w}} L\left(b, \underset{\sim}{w}, \lambda_{i}\right) \right) \end{align*}$$

Slater’s Condition

$$ \underset{b, \underset{\sim}{w}}{\text{arg min}} \frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} \quad \text{subject to } 1-y_{i}\left(\underset{\sim}{w}^{T} \underset{\sim}{x_i} +b\right) \leq 0,\ i = 1, \ldots, N$$$$\begin{align*} \min _{b, \underset{\sim}{w}}\left(\max _{\forall \lambda_{i} \geq 0} L\left(b, \underset{\sim}{w}, \lambda_{i}\right)\right) = \max _{\forall \lambda_{i} \geq 0} \left(\min _{b, \underset{\sim}{w}} L\left(b, \underset{\sim}{w}, \lambda_{i}\right) \right) \end{align*}$$

What’s more, the $b, \underset{\sim}{w}$ are the same

KKT Conditions

For convex optimization problem \\\ \qquad $\displaystyle \underset{b, \underset{\sim}{w}}{\text{arg min}} {\frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} } \quad \text{subject to } {1-y_{i}\left(\underset{\sim}{w}^{T} \underset{\sim}{x_i} +b\right) } \leq 0,\\\\\\ i = 1, \ldots, N$

Denote $\frac{1}{2} \underset{\sim}{w}^T \underset{\sim}{w} $ as $\textcolor{red}{ f_0 }$, $1-y_{i}\left(\underset{\sim}{w}^{T} \underset{\sim}{x_i} +b\right)$ as $\textcolor{red}{f_1, \ldots, f_N}$ . Assume the functions $\textcolor{blue}{f_0,f_1, \ldots, f_N}$ are differentiable. The KKT conditions are \begin{enumerate} \item $\textcolor{blue}{f_i} \leq 0,\ i = 1, \ldots, N$ \item $\lambda_i \geq 0,\ i = 1, \ldots, N $ \item $\lambda_i \textcolor{blue}{f_i} = 0,\ i = 1, \ldots, N $ \item $\displaystyle \nabla \textcolor{blue}{f_0} + \sum_{i=1}^N \lambda_i \nabla \textcolor{blue}{f_i} = 0$ \end{enumerate}

$$\begin{align*} (b, \underset{\sim}{w}) \text{ is optimal } \Leftrightarrow (b, \underset{\sim}{w}) \text{ satisfies KKT conditions } \end{align*}$$$$\begin{align*} & \frac{\partial L}{\partial b}= -\sum_{i=1}^{N} \lambda_{i} y_{i}=0, \quad \frac{\partial L}{\partial w_{k}} = w_{k}-\sum_{i=1}^{N} \lambda_{i} y_{i} x_{i,k}=0 \\\\\\ & \text{where } \underset{\sim}{x_i} = (x_{i,1},\ \ldots ,\ x_{i,n}) \end{align*}$$

\qquad \quad $\frac{\partial L}{\partial b}= -\sum_{i=1}^{N} \lambda_{i} y_{i}=0, \quad \frac{\partial L}{\partial w_{k}} = w_{k}-\sum_{i=1}^{N} \lambda_{i} y_{i} x_{i,k}=0 $

$$\begin{align*} & \underset{\forall \lambda_{i}{\text{arg max}} \geq 0} \left(\min _{b, \underset{\sim}{w}} L\left(b, \underset{\sim}{w}, \lambda_{i}\right)\right) \\\\\\ = & \underset{\forall \lambda_{i} \geq 0}{\text{arg max}} \left(\min _{b, \underset{\sim}{w}}\left(\frac{1}{2} \underset{\sim}{w}^{T} \underset{\sim}{w}+\sum_{i=1}^{N} \lambda_{i}\left(1-y_{i}\left(\underset{\sim}{w}^{T} \underset{\sim}{x_i}+b\right)\right)\right)\right) \\\\\\ = & \underset{\forall \lambda_{i} \geq 0}{\text{arg max} } \left(\min _{b, \underset{\sim}{w}} \left(\frac{1}{2} \underset{\sim}{w}^{T} \underset{\sim}{w}+\sum_{i=1}^{N} \lambda_{i}-\underset{\sim}{w}^{T} \underset{\sim}{w}+0\right)\right) \\\\\\ = & \underset{\forall \lambda_{i} \geq 0}{\text{arg max}} \left(-\frac{1}{2}\left|\sum_{i=1}^{N} \lambda_{i} y_{i} \underset{\sim}{x_i} \right|^{2}+\sum_{i=1}^{N} \lambda_{i}\right) \end{align*}$$

Quadratic Programming

$$\begin{align*} \underset{\forall \lambda_{i} \geq 0}{\text{arg min}} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \lambda_i \lambda_j y_i y_j \underset{\sim}{x_i}^T \underset{\sim}{x_j} - \sum_{i=1}^{N} \lambda_i \\\\\\ & \text{subject to } \sum_{i=1}^{N} y_i \lambda_i = 0 \text{ and } \forall i, \lambda_i \geq 0 \\\\\\ \end{align*}$$

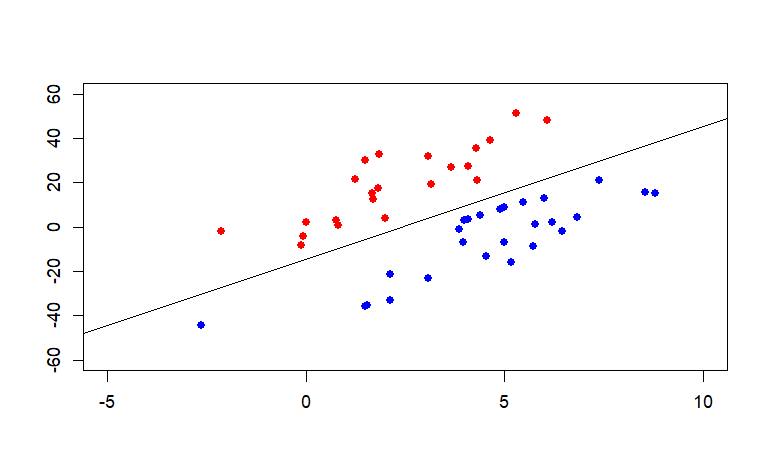
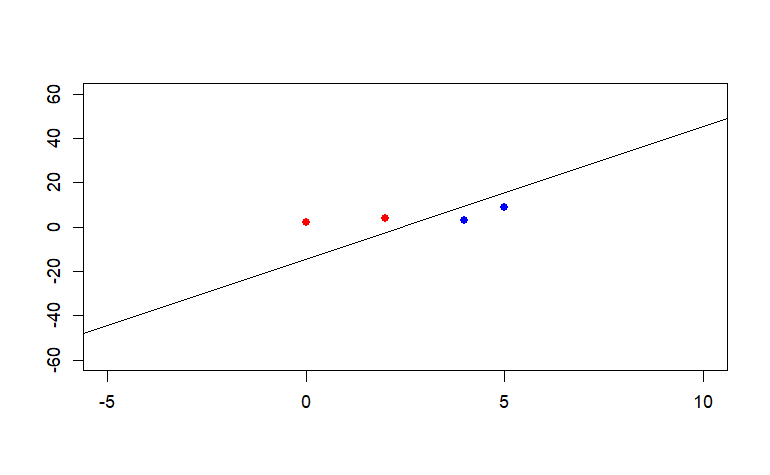
Rewrite as \ $\underset{\forall \lambda_{i} \geq 0}{\text{arg min}} \frac{1}{2} \underset{\sim}{\lambda}^T Q \underset{\sim}{\lambda} + p^T \underset{\sim}{\lambda} \quad \text{ subject to } \underset{\sim}{y^T} \underset{\sim}{\lambda} \geq 0$, $\underset{\sim}{y} \underset{\sim}{\lambda} \leq 0$

$$\begin{align*} Q=\begin{bmatrix} y_1 y_1 \underset{\sim}{x_1}^T \underset{\sim}{x_1} & \cdots & y_1 y_{\scriptscriptstyle N} \underset{\sim}{x_1}^T \underset{\sim}{x_{\scriptscriptstyle N} } \\\\\\ \vdots & \ddots & \vdots \\\\\\ y_{\scriptscriptstyle N} y_1 \underset{\sim}{x_{\scriptscriptstyle N} }^T \underset{\sim}{x_1} & \cdots & y_{\scriptscriptstyle N} y_{\scriptscriptstyle N} \underset{\sim}{x_{\scriptscriptstyle N} }^T \underset{\sim}{x_{\scriptscriptstyle N} } \end{bmatrix} \end{align*}$$

Example

Check the outcome of svm and QP are equal.

4 data points

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
library(CVXR)
d1 <- matrix(c(0, 2, 2, 4, 4, 3, 5, 9), ncol=2, byrow=TRUE)
d2 <- c(1, 1, -1, -1)
# Define the quadratic and linear terms
Dmat <- (d2 %{*}% t(d2)) {*} (d1 %{*}% t(d1))

# 定義變量
x <- Variable(4)
# 定義目標函數和約束條件
objective <- Minimize(0.5 {*} quad_form(x, Dmat) - t(rep(1,4)) %{*}% x)
constraints <- list(x>= 0, x[1]+x[2]-x[3]-x[4] == 0)
# 定義問題
problem <- Problem(objective, constraints)
# 解決問題
result <- solve(problem, solver = "ECOS")
# 顯示結果
print(result$getValue(x))
www=c(0,0)
for (i in 2:4) {
  www = www+result$getValue(x)[i]{*}d2[i]{*}d1[i,]
}

cat("slope=",www[1]/www[2],'\n')
cat("w=",www,'\n')
cat("b=",d2[3]-www%{*}%d1[3,] , '\n')


#2
library(e1071)
# Define the data points and their labels
x <- matrix(c(0, 2, 2, 4, 4, 3, 5, 9), ncol=2, byrow=TRUE)
y <- c(1, 1, -1, -1)

# Train the SVM model
svm_model <- svm(x, y, type='C-classification', kernel='linear', scale=FALSE)
# Get the model parameters
w <- t(svm_model$coefs) %{*}% svm_model$SV
b <- -svm_model$rho
# Print the results
cat('w:', w, '\n')
cat('b:', b, '\n')

# Plot the data and the classification line
plot(x, col=ifelse(y==1, 'red', 'blue'), pch=19,xlim = c(-5,10),ylim = c(-60,60),xlab = "",ylab = "")+
  abline(a = -b/w[2], b = -w[1]/w[2], col="black") +
  abline(a=-(d2[2]-www%{*}%d1[2,])/www[2], b=-www[1]/www[2], col = 1)

cat("svm slope:",-w[1]/w[2],"Qp slope:",-www[1]/www[2], "\n")
cat("svm intercept:",-b/w[2],"Qp intercept:",-(d2[2]-www%{*}%d1[2,])/www[2])

48 data points

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
library(e1071)
library(CVXR)
set.seed(1)
aa = rnorm(20,4,3)
bb = runif(20,0,30)
aabb=cbind(aa, 6{*}aa-21-bb)
cc = rnorm(20,2,3)
dd = runif(20,0,30)
ccdd=cbind(cc, 6{*}cc-8+dd)


# Define the data points and their labels
x <- matrix(c(0, 2, 2, 4, 4, 3, 5, 9, 4.1, 3.5, 4.4, 5.2, 4.9, 8, 6, 13), ncol=2, byrow=TRUE)
x=rbind(x,aabb,ccdd)

y <- c(1, 1, -1, -1,-1,-1,-1,-1,rep(-1,20),rep(1,20))
d1 <- x
d2 <- y
# Define the quadratic and linear terms
Dmat <- (d2 %{*}% t(d2)) {*} (d1 %{*}% t(d1))

# 定義變量
x <- Variable(48)
# 定義目標函數和約束條件
objective <- Minimize(0.5 {*} quad_form(x, Dmat) - t(rep(1,48)) %{*}% x)
constraints <- list(x[1:48]>= 0, x[1]+x[2]-x[3]-x[4]-sum(x[5:28])+sum(x[29:48]) == 0)

# 定義問題
problem <- Problem(objective, constraints)

# 解決問題
result <- solve(problem, solver = "ECOS")

# 顯示結果
print(result$getValue(x))

www=c(0,0)
for (i in 2:4) {
  www = www+result$getValue(x)[i]{*}d2[i]{*}d1[i,]
}

cat("slope=",www[1]/www[2],'\n')
cat("w=",www,'\n')
cat("b=",d2[3]-www%{*}%d1[3,] , '\n')


#2

# Define the data points and their labels
x <- matrix(c(0, 2, 2, 4, 4, 3, 5, 9, 4.1, 3.5, 4.4, 5.2, 4.9, 8, 6, 13), ncol=2, byrow=TRUE)
x=rbind(x,aabb,ccdd)
y <- c(1, 1, -1, -1,-1,-1,-1,-1,rep(-1,20),rep(1,20))

# Train the SVM model
svm_model <- svm(x, y, type='C-classification', kernel='linear', scale=FALSE)
# Get the model parameters
w <- t(svm_model$coefs) %{*}% svm_model$SV
b <- -svm_model$rho

# Print the results
cat('w:', w, '\n')
cat('b:', b, '\n')

# Plot the data and the classification line
plot(x, col=ifelse(y==1, 'red', 'blue'), pch=19,xlim = c(-5,10),ylim = c(-60,60),xlab = "",ylab = "")+
  abline(a = -b/w[2], b = -w[1]/w[2], col="black") +
  abline(a=-(d2[2]-www%{*}%d1[2,])/www[2], b=-www[1]/www[2], col = 1)

cat("svm slope:",-w[1]/w[2],"Qp slope:",-www[1]/www[2], "\n")
cat("svm intercept:",-b/w[2],"Qp intercept:",-(d2[2]-www%{*}%d1[2,])/www[2])

Reference

Convex Optimization
Method of Lagrange Multipliers
線代啟示錄
 Karush-Kuhn-Tucker conditions pdf
Karush-Kuhn-Tucker conditions
林軒田-機器學習技法
 An Idiot’s guide to Support vector machines
Support Vector Machine(with Numerical Example)
A Tutorial on Support Vector Machines for Pattern Recognition
Machine Learning Basics
RPubs SVM