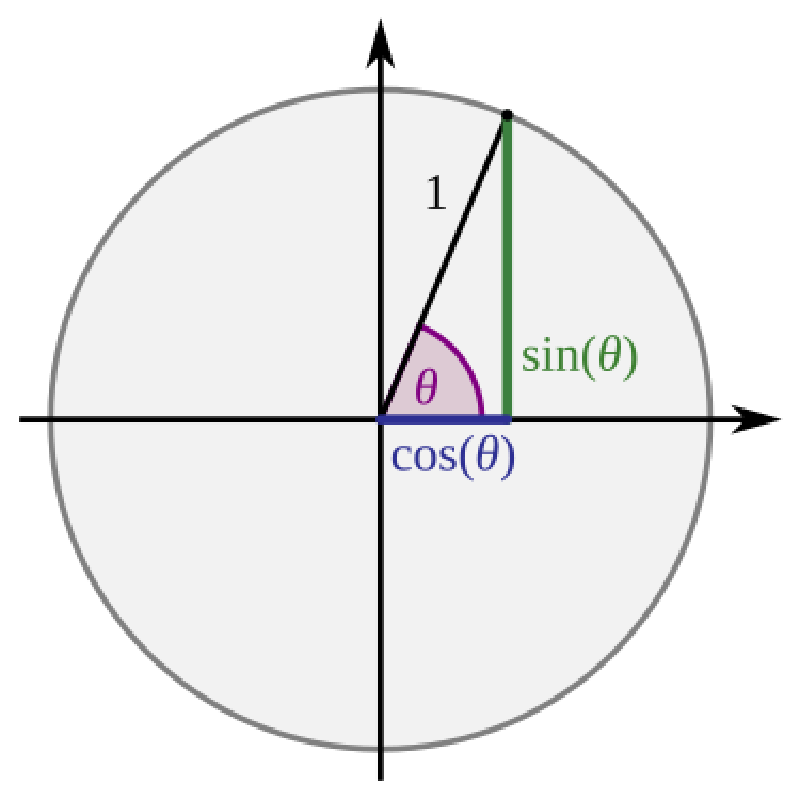
Background In complex plane, x-axis, y-axis are R \mathbb{R} R i = − 1 i=\sqrt{-1} i = − 1 2 + 3 i 2+3i 2 + 3 i ( 0 , 0 ) (0,0) ( 0 , 0 ) ( 2 , 3 ) (2,3) ( 2 , 3 ) z 1 ⇀ , z 2 ⇀ \overset{\rightharpoonup }{z_1}, \overset{\rightharpoonup }{z_2} z 1 ⇀ , z 2 ⇀
z 1 ⇀ = cos θ 1 + i sin θ 1 = ( cos θ 1 , sin θ 1 ) z 2 ⇀ = cos θ 2 + i sin θ 2 = ( cos θ 2 , sin θ 2 ) \begin{align*}
& \overset{\rightharpoonup }{z_1} = \cos{\theta_1}+ i\sin{\theta_1} = (\cos{\theta_1}, \sin{\theta_1}) \\
& \overset{\rightharpoonup }{z_2} = \cos{\theta_2}+ i\sin{\theta_2} = (\cos{\theta_2}, \sin{\theta_2})
\end{align*} z 1 ⇀ = cos θ 1 + i sin θ 1 = ( cos θ 1 , sin θ 1 ) z 2 ⇀ = cos θ 2 + i sin θ 2 = ( cos θ 2 , sin θ 2 ) Identities in Complex Plane In complex plane, vector z 1 ⋅ z 2 z_1 \cdot z_2 z 1 ⋅ z 2 ∣ z 1 ∣ ∣ z 2 ∣ |z_1||z_2| ∣ z 1 ∣∣ z 2 ∣ θ 1 + θ 2 \theta_1+ \theta_2 θ 1 + θ 2
z 1 ⇀ ⋅ z 2 ⇀ = cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) = ( cos θ 1 + i sin θ 1 ) ⋅ ( cos θ 2 + i sin θ 2 ) = ( cos θ 1 cos θ 2 + i 2 sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) = ( cos θ 1 cos θ 2 − sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) \begin{align*}
\overset{\rightharpoonup }{z_1} \cdot \overset{\rightharpoonup }{z_2}
&= \cos{(\theta_1+\theta_2)}+ i\sin{(\theta_1+\theta_2)} \\
&= (\cos{\theta_1}+ i\sin{\theta_1}) \cdot (\cos{\theta_2}+ i\sin{\theta_2}) \\
&= (\cos{\theta_1} \cos{\theta_2} +i^2 \sin{\theta_1} \sin{\theta_2}) + i(\cos{\theta_1} \sin{\theta_2}+ \sin{\theta_1} \cos{\theta_2}) \\
&= (\cos{\theta_1} \cos{\theta_2} - \sin{\theta_1} \sin{\theta_2}) + i(\cos{\theta_1} \sin{\theta_2}+ \sin{\theta_1} \cos{\theta_2})
\end{align*} z 1 ⇀ ⋅ z 2 ⇀ = cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) = ( cos θ 1 + i sin θ 1 ) ⋅ ( cos θ 2 + i sin θ 2 ) = ( cos θ 1 cos θ 2 + i 2 sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) = ( cos θ 1 cos θ 2 − sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) Therefore, we explain the formula
cos ( θ 1 + θ 2 ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 sin ( θ 1 + θ 2 ) = cos θ 1 sin θ 2 + sin θ 1 cos θ 2 \begin{align*}
& \cos{(\theta_1+\theta_2)} = \cos{\theta_1} \cos{\theta_2} - \sin{\theta_1} \sin{\theta_2} \\
& \sin{(\theta_1+\theta_2)} = \cos{\theta_1} \sin{\theta_2}+ \sin{\theta_1} \cos{\theta_2}
\end{align*} cos ( θ 1 + θ 2 ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 sin ( θ 1 + θ 2 ) = cos θ 1 sin θ 2 + sin θ 1 cos θ 2 Reference